1、材质介绍
在百度百科中材质是这样定义的,材质是指物体看起来是什么质地,材质可以看成是材料和质感的结合。材质在渲染程式中,它是表面各可视属性的结合,这些可视属性是指表面的色彩、纹理、光滑度、透明度、反射率、折射率、发光度等。正是有了这些属性,才能让我们识别三维中的模型是什么做成的,也正是有了模型材质。
与材质容易混淆的另外两个概念是纹理和贴图:首先我们看纹理,纹理的英文是Texture,它的翻译特别好,花纹肌理,纹理在图形学中表示的就是物体表面的图案花纹或者一些物理信息,比如凹凸感。然后我们来看看贴图,贴图的英文名是Maping,是指一种映射关系,计算机图形学上就是只将纹理按照一定的规则映射到物体上。
所以基本上我们可以这样理解,材质(Material)是物体表面的属性集,贴图(Mapping)是纹理相关的映射关系,纹理(Texture)是指具体的渲染信息。他们的关系基本上就是材质包含贴图,贴图包含纹理。比如一个材质中可能用漫反射贴图、法线贴图,而相应贴图有指定了对应的纹理。
2、PBR材质
PBR全称是Physicallly-Based Rendering,所以PBR材质就是指基于物理渲染的材质。如果想要理解PBR材质的含义,我们就要知道基于物理具体是指什么。
在现实生活中,物体显示出颜色通常由两个因素决定:自身因素和外部因素,其中外部因素绝大部分是由光照来决定的;因此想要基于物理我们就需要关注物体本身和光照这两个方面。首先对于物体本身,我们要考虑物体表面不可能是绝对光滑的平面,所以需要我们引入微表面理论,基于微表面进行研究;然后我们需要关注光的物理性质,光包括了颜色、光通量、光强度、光亮度等等一系列概念,拥有诸如反射、折射等性质,还会产生诸如菲涅尔等效果;此外在光与物体交互时,要考虑光线可能发生遮挡,也可能被吸收,要遵循能量守恒定律。所以概括来说就是在遵循微表面理论,光学特性和能量守恒的前提下,根据物体本身特性通过数学推算出的物体表面的属性集我们就叫做PBR材质。
说到PBR材质,我们在应用过程中不得不说的就是金属度和粗糙度两个属性,通常情况下,我们都会根据这两个属性值然后和相关贴图一起来构建我们的PBR材质。那这两个特属性到底是如何作用于PBR材质的呢,我们记下来会延续上一节,通过对cook torrence 模型中提到的F、G、D函数加以说明。
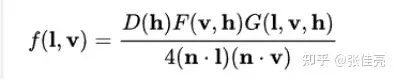
3、菲涅尔函数(F)
3.1菲涅尔效应
我们站在湖边,如果我们看脚下,那我们可以清楚的看到河底的小石子,如果我们看向远方,那么湖面上显示的就是美丽的倒影,这种现象就叫做菲涅尔效应。具体原因是光线在从一种折射率的物体向另一种折射率的物体进行传播时,会在二者交界处同时发生反射和折射,而反射折射的比例会随着入射角的不同而不同。
我们在渲染物体时,也需要考虑光线照射物体同时发生反射和折射的情况,这时我们就需要计算出反射和折射的占比,而菲涅尔函数(菲涅尔方程)就是用来描述这种情况下反射和折射的比例的。
3.2 菲涅尔方程
由于我们看到的一般都是物体反射光,所以我们只需要关注反射所占比例即可。
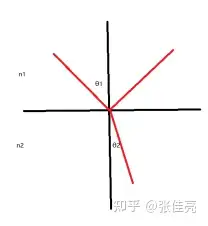
上图表示光从折射率n1的物体向折射率为n2的物体传播,入射角为θ1,折射角为θ2,那么在光学中有如下公式:
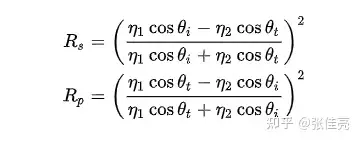
其中Rs和Rp分别是入射光的S偏振和p偏振所产生的反射比,同时由于图形学中不考虑偏振,所以我们认为二者是等量的,所以有
R = (Rs + Rp) / 2
以上公式只用于电介质,导体的菲涅尔方程更复杂,且不同波长表现不一致。
3.3 Schlick近似
鉴于导体的菲涅尔方程更复杂,所以Schlick提出了近似函数
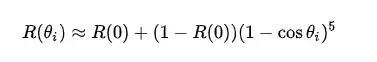
其中R0为基础反射率,即光线垂直入射时的反射率,θi为视点方向和法线方向的夹角,因此可推导出如下公式
FSchlick(n,v,R0)=R0+(1−R0)(1−(n⋅v))5
至此我们发现只要知道物体的基础反射率,那么我们就能很容易的求得函数值,下图是不同物体的基础反射率的列表
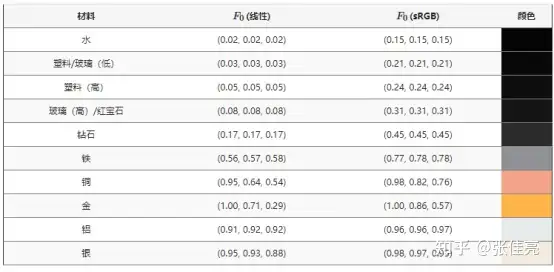
通过对上表进行观察,我们可以发现金属和非金属的基础反射率存在如下差异:
非金属的三个颜色分量基础反射率一致,金属不一致非金属的基础反射率低,金属的高PS:因为金属和非金属在菲涅尔效应上的不同特性,物理学上将金属称为导体(Conductor),非金属称为电介质(Dielectric),电介质这个名字笔者也很陌生,还很容易和电解质弄混
由于金属和非金属的基础反射率表现不一致,为了能够统一起来,就提出了金属度metalness的概念,金属度表示一个物体金属性的占比,通过金属度来得出物体的基础反射率,公式如下:
vec3 R0 = vec3(0.04);
R0 = mix(R0, surfaceColor.rgb, metalness);
如果是电介质则可以使用自身的R0,金属则可以使用0.04,0.04是一个经验值。
3.4小结
到此我们可以知道,PBR材质的金属度参数是用来计算材质对应物体的基础反射率的;进而根据进出反射率R0,可以通过Schlick近似函数求出近似的反射比,最后根据反射定律得出反射所贡献的物体颜色值。
4. 法线分布函数(D)
4.1微表面模型
由于现实世界中是不存在绝对光滑的表面的,所以对物体表面的表示就引入了微表面模型。微表面模型认为物体表面是由无限多个微表面组成的,而这些微表面是绝对光滑的,但是微表面的朝向按照一定规律分布,和物体表面不一致,各个微表面彼此的朝向也可能不一致,这种不一致就导致了物体表面的粗糙感。
由于微表面的朝向不一致,所以当光线照射物体表面时,只有法线位于入射方向和视角方向中间的那部分微表面才能将光线反射到观察者眼中。因此要知道能够看到多少反射光线,我们就需要计算出这部分微表面的占比,即需要知道微表面的法线分布情况,法线分布函数就是用来描述微表面的法向分布情况的。
4.2 法线分布函数
法线分布函数英文全称为Normal Distribution Function,缩写为NDF。通俗来讲,法线分布函数就是用来求微表面中法向量m和半程向量h一致的微平面面积占宏表面比例的函数,该函数可以反应宏平面的光滑程度,从而影响观察点真正接受到有效光通量的多少。
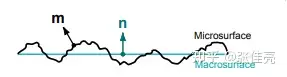
上图为一个微表面的示意,m为微表面的法向量,n为宏表面的法向量,通常我们将二者的夹角称之为NoH,用θ来表示,而物体表面的粗糙度我们用a来表示,半程向量(blin-phong:L+V)用h来表示。
目前NDF有很多种,很少有人能够或者说有必要全部熟悉,我们这里只看一下UE中应用的几个即可,这里给出的都是各项同性的函数代码,至于各项同性和各向异性的概念会在后面章节讲述,实现如下图:

4.3 小结
由此我们可以看到,pbr材质上的粗糙度属性是用来计算材质微表面的法线分布的,我们可以通过调整材质本身的粗糙度属性来影响到NDF函数返回值得大小,从而影响到BRDF的结果,最终反映到观察的颜色上来。
5. 几何函数(G)
5.1 自遮挡现象
我们上一节说到通过D函数,我们能够找到m等于h的微平面,那么这些微平面都能把入射光传递到视点么,其实不尽然,我们可以看一下下图:

假设我们图中两个红色的微平面是同h朝向一致的,但是由于入射光方向被遮挡或者出射光方向被遮挡,实际上都不能够将光照传递给视点,也就是发生了自己遮挡自己的现象。在基于物理的渲染技术中,几何函数(Geometry Function)可以用来描述微平面自遮挡的属性,表示具有和好同向的微平面中,同时不被入射方向 和出射方向遮挡的占比。
5.2几何函数
几何函数,英文为Geometry Function,也叫几何遮蔽函数、几何阴影函数等,几何函数也种类繁多,比如Smith,V-cavity(Cook-Torrance),Schlick-Smith、Neumann、kelemen、Implicit等等,我们这里不一一介绍,同样我们只看一下UE中的应用,如下图:

其中a为粗糙度,NOV为视点方向和宏表面法向的夹角,NOL为光源方向与发现的夹角。
5.3 小结
由此我们可以看到,pbr材质上的粗糙度属性同时也可以用来计算材质微表面的自遮挡,我们可以通过调整材质本身的粗糙度属性来同时影响到D函数和G函数返回值得大小,进而影响到BRDF的结果,最终反映到观察的颜色上来。
6.总结
综上,我们可以知道所谓PBR大体就是基于微平面、光学等理论,在能量守恒的前提下进行的渲染技术,通常都是基于BRDF来计算得来的;而PBR材质就是在PBR下通过给出的诸如粗糙度、金属度等属性来通过影响BRDF而最终得到和物理世界接近的颜色表现的材质。
7.参考文献
https://zhuanlan.zhihu.com/p/31534769
https://www.cnblogs.com/wickedpriest/p/13363205.html


网友评论
最新评论