其实这个问题看似简单，也很有趣味，下面我从理论角度分析一下原因：

在进行下面推导的过程之前，先有几点说明：

1）试管底面的形状对计算结果没有影响；

2）试管不是密封的，试管内的水适量；

3）水没有从试管里面流出。

下面以试管倾斜的情况为研究对象，进行截面尺寸的绘制，如下图：

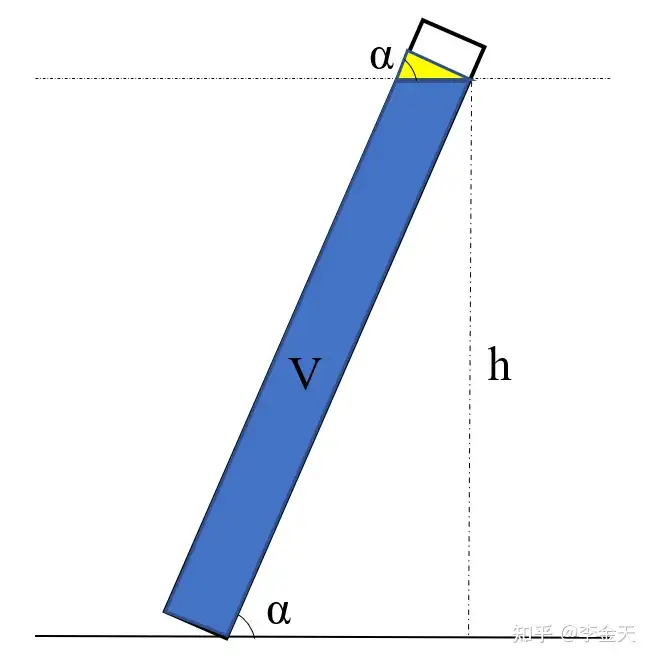
设试管的半径为 rr ，试管倾斜的角度为 α\alpha ，试管所装水的体积为 VV ，倾斜时试管中所装水的高度为 hh 。其中当试管垂直时，试管中水的液面高度为 h0h_{0}，即当 α=90°\alpha=90° 时，h=h0h=h_{0}。

由上图可知，无论试管如何倾斜，试管内溶液的体积一直保持不变，即为蓝色区域的面积。面积的算法为圆柱体积剪去黄色三角形的体积，计算公式如下：

hsinαπr2−12πr22rtanα=V\frac{h}{sin\alpha}\pi r^{2}-\frac{1}{2}\pi r^{2}\frac{2r}{tan\alpha}=V

即：

h=Vπr2sinα+rcosαh=\frac{V}{\pi r^{2}}sin\alpha+rcos\alpha

根据三角函数和差公式得：

h=V2+π2r6π2r4sin(α+θ),tanθ=πr3Vh=\sqrt{\frac{V^{2}+\pi^{2}r^{6}}{\pi^{2}r^{4}}}sin(\alpha+\theta), tan\theta=\frac{\pi r^{3}}{V}

当 α=90°\alpha=90° 时， h=h0h=h_{0} , V=πr2h0V={\pi r^{2}}{h_{0}}

即:

tanθ=rh0tan\theta=\frac{r}{h_{0}}

查阅资料得试管的定义如下：

根据一般试管的规格，设试管内所装水的初始高度与试管的长度接近，可知：

，tanθ=0.05，θ=arctan0.05=2.86°tan\theta=0.05，\theta=arctan0.05=2.86°

即：

h=V2+π2r6π2r4sin(α+2.86°)h=\sqrt{\frac{V^{2}+\pi^{2}r^{6}}{\pi^{2}r^{4}}}sin(\alpha+2.86°)

其中 α0<α<90°\alpha_{0}<\alpha<90° ， α0\alpha_{0} 为水即将流出但未流出的临界角度，试管的倾斜角度。

由上式可知，试管内液体的高度先增加后减小，只是这个增加的部分很难察觉的到，因为我们倾斜试管的速度相对很快，在不察觉中，这个增加的过程就已经过去了。

所以对于试管而言，从垂直角度到倾斜87.14°的的过程中，试管内水的液面高度是增加的，涨幅为0.86%，而从87.14°到 α0\alpha_{0} ，试管内水的液面高度一直递减。

以上结论仅仅适用试管，如果应用到其他容器，只需将其他容器的半径和初始高度的比值计算出来，带入上式即可。

以上结论皆为